Applied AIML Data Science

Data science and AI/ML for business value

about me                 home

Market Cycle Prediction Model

Strategy Backtest 2020

published December 31, 2020

Introduction

This article is the third part of a three-part series of articles with the overriding goal of developing an ML model that predicts Bear and Bull market cycles. The model is useful on its own as a buy-sell signal, as input to broader investment strategy, or for use as an input to another financial model. Furthermore, the same process used here to model the S&P 500 index also works for individual securities. Such a market cycle prediction model is not available to the open-source community. Thus, an additional two objectives are to build the model based on open-source financial data, and to publish the model and methods to the open-source software community.

The articles in this series include the following:

In this article, we begin by loading the ML dataframe developed in the previous article (Market Cycle Model - Data Analysis) followed by preparing the ML training and test data. We will then use supervised learning methods to train several tree-based predictive models, including a Decision Tree, Random Forest, and XG Boost classification models. While training the models, we will select the ML features to optimize predictive performance. We consider feature importance and multi-collinearity for selecting the ML features. The training performance is measured in the form of Accuracy, Recall, and Precision.

The ML models achieve a high degree of accuracy, where XG Boost, the best performing model, achieves accuracy above 99% and recall and precision above 98%. Next, the financial performance is gauged with financial backtesting. The levels of accuracy achieved are successful for anticipating all historical bear markets going back to 1957. The models provide a significant improvement in investment performance when compared to an S&P 500 index. In addition to the raw model output, a smoothed prediction is generated to avoid short-term buying and selling, such as sell one day and buy the next. A 5-day smoothing is sufficient for eliminating short-term trading over the market history going back to 1957. This article and the article series is concluded with a summary of all three articles.

Outline

This article includes the following sections.

Github Links

The software and notebooks discussed in this article are available in the following Github locations.

Notebook Initialization

The ML notebook is initialized with a few packages, including Pandas, Numpy, Matplotlib, and Datetime. We also run inline the fmml and fmplot modules. The fmml module contains several functions developed for creating an ML predictive model from stock market time-series ML Features. The fmplot module includes functions that make it easy to plot time-series stock market data. We will demonstrate how to use both of these modules in this article. Several examples for the fmplot module were given in the first article, and additional examples are included in this article.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime as dt
%run fmml
%run fmplot

Import the ML DataFrame

In the previous article, we processed the S&P 500 data and created machine learning features, followed by saving the corresponding dataframe to a file. The dataframe contains ML features and training labels (i.e., the mkt variable) plus other dependent variables. Below, we read in the dataframe and then further process it and develop our ML model.

A couple of data manipulations are made at this stage. By evaluating some initial ML models, it is observed that the T10Y3M variable does not contribute to model accuracy, so it is dropped. Since the T10Y3M variable is available from 1982 forward, it is useful to drop it so that the ML prediction can start earlier. The consumer sentiment is available from 1953, so it will limit the start of the ML prediction data. Additionally, the feature extraction contains several long term averages resulting in an initial processing period without useful data. Thus, the data start date is set to 1955.

filename='./data/df_ml_2020115_195013_to_2020114.csv'
dfMLXY = pd.read_csv(filename,index_col=0,parse_dates=True)
print(dfMLXY.shape)
dfMLXY.drop('T10Y3M',axis=1,inplace=True)
dataStartDate=dt.datetime(1955,1,1)
dfMLXY=dfMLXY.loc[dataStartDate:]

Data Preprocessing

We begin by extracting the training labels (Y) and ML features (X) from the dfMLXY dataframe. Some of the columns in the DataFrame are not ML Features and are dropped. The ML features are standardized, such that they are transformed to zero-mean with a standard deviation of one with the SciKit StandardScaler(). It is worth noting tree-based models do not require variable standardization. Here we include the standardization out of best-practice in the case at a future time we want to evaluate the performance of a non-tree based model.

Many of the ML features are averages over differing window lengths and will have a maximum correlation to a target variable sometime in the future. For example, moving average with a window length of N will be maximally correlated to the target variable N/2 days in the future. These alignment relationships are studied in the second article. The mlalign() function, contained in the fmml module, will align the variables so that the resulting dataframe row contains feature variables that are maximally correlated to the target variable. The mlalign() function takes as input a list of 2-tuples. The tuple’s first parameter is an integer n corresponding to a correlation to the target variable n days in the future. The second parameter of the tuple is a list of features corresponding to n.

# Y Dataframe
dfY=pd.DataFrame(dfMLXY['mkt'])
dfY.rename(columns={'mkt':'y'},inplace=True)
dfY['y']=(dfY['y']+1)/2
print(dfY.shape)

# X Dataframe
dfX = dfMLXY.drop(['Close','High','Low','Open','Volume','mkt','mcnr','Earnings','GDP'],axis=1)
x_columns=dfX.columns

SScaler=StandardScaler()
X=SScaler.fit_transform(dfX)    
dfX=pd.DataFrame(data=X, columns=dfX.columns, index=dfX.index)
print(dfX.shape)


NshiftFeatures = [(1 , ['mcupm','mucdown','mdcup', 'CPIAUCSL', 'cpimom','UMCSENT','umcsent_pchange',
                 'UNRATE','unrate_pchange','recession1q','recession2q','PE','PE_mom','gdp_qoq',
                'Close_nma1','Volume_nma1']),
                (3, ['Close_nma5','Volume_nma5'] ),
                (5,['Close_nma10','Volume_nma10']),
                (7,['Close_nma15','Volume_nma15']),
                (10,['Close_nma20','Volume_nma20']),
                (15,['Close_nma30','Volume_nma30']),
                (20,['Close_lrstd25','Close_lrstd25_avgvel5']),
                (25,['Close_nma50','Volume_nma50','NDI50','PDI50','ADX','rma_sma20_sma50']),
                (50,['Close_lrstd63','Close_lrstd63_avgvel5']),
                (100,['Close_lrstd126' , 'Close_nma200','rma_sma50_sma200','Volume_nma200','Close_lrstd126_avgvel5'])
                ]

dfXaligned,dfYaligned = ml_align(dfX,dfY,NshiftFeatures)

Above, we read in an ML dataframe with 52 columns. We next build an ML model by noting the feature importance and multi-collinearity with other features. For example, each model, Decision Tree, Random Forest, and XG Boost, will result in a different ML Features set. Below, the features to be eliminated for each model are placed into a list.

dt_low_imp_cols =['unrate_pchange_n0', 'Volume_nma1_n0', 'Close_nma10_n4', 'recession2q_n0', 'Volume_nma30_n14',
                  'Volume_nma5_n2', 'Close_lrstd25_avgvel5_n19', 'Volume_nma50_n24', 'cpimom_n0', 'recession1q_n0',
                  'Volume_nma15_n6', 'Close_lrstd126_avgvel5_n99', 'Volume_nma10_n4', 'Close_nma1_n0',
                 'Close_nma30_n14', 'NDI50_n24', 'Close_lrstd63_avgvel5_n49', 'Close_nma200_n99']


rf_xgb_low_imp_cols =['recession2q_n0','Volume_nma5_n2', 'Volume_nma1_n0', 'Close_nma1_n0','Volume_nma15_n6',
                 'Close_lrstd25_avgvel5_n19','Close_lrstd63_avgvel5_n49', 'Close_lrstd126_avgvel5_n99',
                 'Volume_nma20_n9','Close_nma20_n9','Close_nma5_n2', 'Volume_nma50_n24',
                 'Close_nma15_n6']

rf_low_imp_cols =  rf_xgb_low_imp_cols + ['Volume_nma10_n4', 'recession1q_n0',
                                          'Volume_nma30_n14', 'Close_nma30_nd14' ]

xgb_low_imp_cols = rf_xgb_low_imp_cols + ['NDI50_n24', 'ADX_n24', 'PDI50_n24', 'Close_nma50_n24', 'cpimom_n0',
                                          'Close_lrstd25_n19',  'Volume_nma30_n14',  'Close_nma30_n14']
# Combine all cols to be dropped
low_imp_cols=xgb_low_imp_cols


print('low imp cols = ',low_imp_cols)
print("num low importance cols =",len(low_imp_cols))

Model Train and Test

The fmclftraintest() function from the fmml module facilitates training and testing the market cycle classification model. The mkt parameter indicates that the market is in a Bull or Bear condition, and is thus the training label. The function takes as input the ML Features contained in the dfXaligned dataframe (after droping low importance variables), the training labels in the dfYaligned dataframe, and a prediction start date and end date. Additionally, it receives as input the type of model to build. The modeltraindays parameter causes the the model to be trained daily, after the market close.

Training Procedure

The model is trained to forecast one day forward. The training and prediction procedure is encapsulated in the fmclftraintest() function, and works as follows. For example, suppose we want a prediction for Wednesday, January 8, 2020. The training data is prepared, one set of ML Features per trading day, up to two market days (Monday, January 6) before the prediction. The market results (“labels”) are paired with ML Feature rows. The model is trained to predict one day forward, so the market result (label) from January 7 is paired with the ML feature row on January 6. The model is trained with supervised learning to predict one day forward, up to January 7. After the model is trained, the ML features on January 7 (after market close) are input to the model to create buy-sell prediction (classifier output). The model output predicts the mkt variable for the close of trading on Wednesday, January 8.

Next, at the close of trading on January 8, we would like a prediction for January 9. There is now one additional day of training data available. A new model is trained using all available data up to two market days (Tuesday, January 7) before the prediction and using the training labels until January 8. A market prediction is made for January 9 using the ML Features from January 8. This cycle continues each day, training a new model with all available data up to two days before and predicting (i.e., forecast) one day forward.

In the code block below, we train a model with the first prediction corresponding to January 2, 1957, and the last prediction on November 4, 2020. Due to the feature alignment, the training features are available from 1955-5-23 forward. Training labels are available up until November 3, 2020. The fmclftraintest() function displays helpful information as it starts and as it trains and predicts. For example, below the code block is listed the model specified, the training data start date, the first prediction date, and performance until 1958-1-1. At the beginning of each year, it displays the model performance results so far. The fmcltraintest() function returns the training results dataframe dfTR, which contains the prediction p_1 (prediction one day forward). Also returned is the dfXYTR data frame, which is the dfTR dataframe (prediction results) merged back into a composite dataframe containing ML Features, training labels, and prediction results. The dfXYTR dataframe is useful for analyzing and studying the prediction results along with the ML Feature set.

predict_s = dt.datetime(1957,1,2)
predict_e = dt.datetime(2020,11,4)
model='XGB' #
print("...")
nmodeltraindays=1

dfTrain=dfXaligned.drop(low_imp_cols,axis=1)

print('dfTrain.shape =',dfTrain.shape)  
print('dfTrain.columns =',dfTrain.columns)
dfXYTR,dfTR,clf = fmclftraintest(dfTrain,dfYaligned,'y_1',predict_s,predict_e, model=model,modeltrain_ndays=nmodeltraindays,v=1)

#display(dfTR[['p_1','y_1','model_date']].tail(10))
# Join the training results with some of the original data
# needed for analyzing and visualizing
dfxyp=dfMLXY[['Close','Volume','High','Low','PE','Earnings',
              'mcnr','mcupm','mdcup','mucdown','mkt']].join(dfXYTR[['p','y_1','p_1','model_date']],lsuffix='l',rsuffix='r', how='outer' )

# Smooth with N-day (Nsmooth) rolling window
Nsmooth=4
dfxyp=binarysmooth(dfxyp,'p_1',NW=Nsmooth , y_s='p_s_1')
dfxyp['p_s']=dfxyp['p_s_1'].shift(1) # shift results one day forward for easy comparison to non-shifted training labels

dfTrain.shape = (16772, 20)
dfTrain.columns = Index(['mcupm_n0', 'mucdown_n0', 'mdcup_n0', 'CPIAUCSL_n0', 'UMCSENT_n0',
       'umcsent_pchange_n0', 'UNRATE_n0', 'unrate_pchange_n0',
       'recession1q_n0', 'PE_n0', 'PE_mom_n0', 'gdp_qoq_n0', 'Close_nma10_n4',
       'Volume_nma10_n4', 'rma_sma20_sma50_n24', 'Close_lrstd63_n49',
       'Close_lrstd126_n99', 'Close_nma200_n99', 'rma_sma50_sma200_n99',
       'Volume_nma200_n99'],
      dtype='object')
train after every k = 1 days
predict start date = 1957-01-01
predict end date =  2020-11-04
model = XGB
first training sample = 1955-05-23
train samples available = 412

1958-01-01 train samples = 667
  samples = 667, pos samples = 312, neg samples = 355
  accuracy =  0.996
  precision (tp /(tp + fp)) = 0.995
  recall tp /(tp + fn) = 1.000
  fscore = 2*precision*recall / (precision + recall) = 0.998
  tp = 207 fp = 1 tn = 49 fn = 0

As we see in the code block (above), at the conclusion of training and prediction, additional variables are joined into the dataframe. In order to remove any short term buy-sell changes the prediction is smoothed over a 5-day rolling window.

Training Results

The model results, confusion matrix, accuracy, recall, and f1 score are derived with the help of the fmclfperformance() function. The model results are very good achieving an accuracy of 99.5%, recall of 98.7%, and precision of 98.2%. These results are very encouraging indeed. The ultimate test of the model will be how well it performs in financial back testing.

(accuracy,precision,recall,fscore,dfcma,dfcmr,tp,fp,tn,fn)=fmclfperformance(dfTR,'y_1','p_1')


Predicted Positive	Predicted Negative	Totals
actual Positive	    2673	     49	       2722
actual Negative	    36	      13603	     13639
accuracy      =   0.995
errors        =   85
total samples =   16361
precision (tp /(tp + fp)) =   0.987
recall tp /(tp + fn)      =   0.982
fscore = 2*precision*recall / (precision + recall) =  0.984
tp = 2673 fp = 36 tn = 13603 fn = 49

From Predictions to Buy-Sell Investments

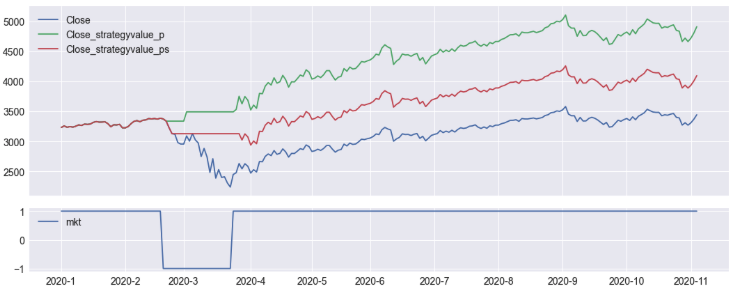
The model identifies all Bear and Bull markets from the start of prediction in 1957 through November 2020. Figure 1 (a) and (b) the prediction results from 2000 to 2020 are displayed. Figure (a) illustrates the normalized Bull and Bear returns, the “truth” label mkt, prediction p_1 (1 day forward prediction), and smoothed prediction p_s_1. Though it has a high degree of precision, recall, and accuracy, the raw prediction output from the model, shows a few places with short-term up and low periods. Often it is desirable to eliminate such periods to avoid short-term investment or de-investment. The smoothed prediction p_s_1 takes the 5-day rolling mean of the p_1 signal. If the mean is above 0.5 then p_s_1 = 1, else p_s_1 = 0. This smoothing approach is successful in eliminating all short-term predictions. The result is once p_s_1 switches from Bull to Bear (or visa-versa), it remains there until the next market switch.

The buy-sell trading strategy is described with reference to Figure 1 (b). The graph illustrates the S&P market close price, the mkt condition (1 = Bull, -1 = Bear), the prediction p_1, and smoothed prediction p_s_1 from February 2020 to November 2020. For example, to avoid short-term buying and selling, consider buying and selling an S&P 500 index with the p_s_1 signal. The market hit’s the Bull market high on February 19 with a Close Price of $3,386.15, and the market condition (mkt) changes to Bear (downward trend) on February 20. Two market days later (February 21, end-of-day), p_1 goes from 1 to 0, signaling to de-invest (i.e., “sell”) at the price of 3,337.23. One market day later, February 25, p_s_1 = 0 signaling to de-invest at 3,128.21. The market continues to fall, hitting a low on March 23 of 2,237.4. On March 24, the market condition (mkt) changes to Bull (upward trend). The smoothed model output p_s_1 = 1 at the end of day March 26, signals to invest. In the ideal case, an investment (“buy”) is made before opening on March 27. The buy price is approximated to be the March 26 close price of 2,630.07 with an investment of 3,128.21 according to the previous p_s_1 sell signal. The market value is sustained at the previous sell price and is re-invested as of March 26 close, before opening on March 27.

s=dt.datetime(2000,1,1)
e=dt.datetime(2020,11,4)

fmplot(dfxyp,['mcnr','mkt','p_s','p_1'], plottypes =['mktcycle','line','line','line'],
       startdate=s, enddate=e, sharex=True, llocs=['upper left', 'upper right','upper right', 'upper right'],
       figsize=(18,7),ytick_labelsize=14, xtick_labelsize=14, legend_fontsize=14,
       height_ratios=(3,1,1,1), xlabel = '(a)' , xlabelfontsize=16, xlabelloc=(0,-0.6))



s=dt.datetime(2020,2,1)
e=dt.datetime(2020,11,4)
fmplot(dfxyp,['Close','mkt','p_s_1','p_1'], startdate=s, enddate=e, sharex=True,
       llocs=['upper right', 'upper right','upper right', 'upper right'],
      figsize=(18,7),ytick_labelsize=14, xtick_labelsize=14, legend_fontsize=14,
       height_ratios=(3,1,1,1), xlabel = '(b)' , xlabelfontsize=16,  xlabelloc=(0,-0.6))

dfxyp[['Close','mkt','p_s_1','p_1']][dt.datetime(2020,2,18):dt.datetime(2020,3,5)]


Date		    Close	     mkt_1	 p_1   p_s_1		
020-02-18	  3370.29	   1.0	 1.0	 1.0
2020-02-19	3386.15	  -1.0	 1.0	 1.0
2020-02-20	3373.23	  -1.0	 1.0	 1.0
2020-02-21	3337.75	  -1.0	 0.0	 1.0
2020-02-24	3225.89	  -1.0	 0.0	 1.0
2020-02-25	3128.21	  -1.0	 0.0	 0.0
...
2020-03-19	2409.39	  -1.0	0.0	   0.0
2020-03-20	2304.92	  -1.0	0.0	   0.0
2020-03-23	2237.4	   1.0	0.0	   0.0
2020-03-24	2447.33	   1.0	1.0	   0.0
2020-03-25	2475.56	   1.0	1.0	   0.0
2020-03-26	2630.07	   1.0	1.0	   1.0
2020-03-27	2541.47	   1.0	1.0	   1.0
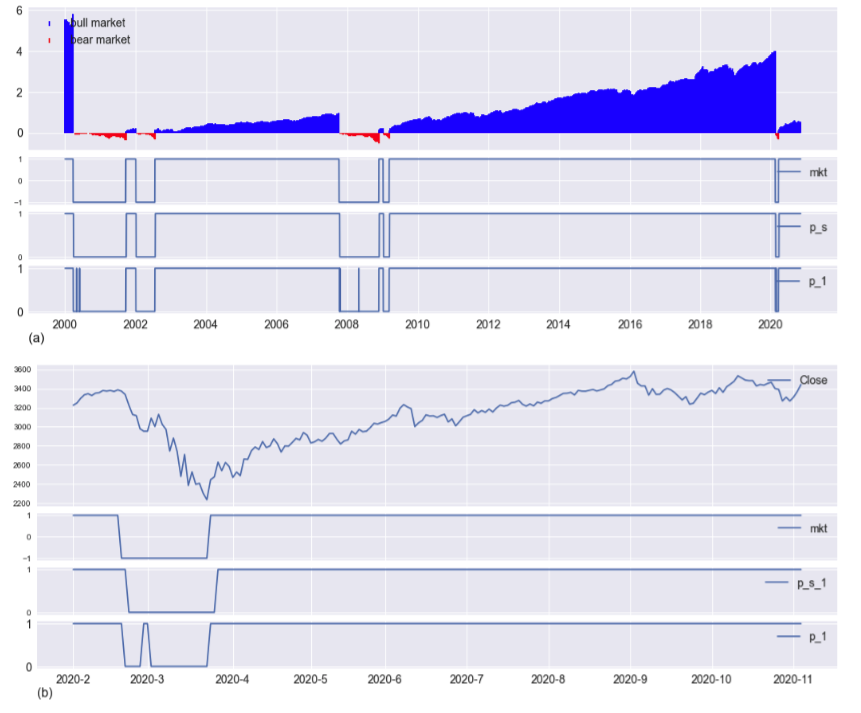
Market Cycle Prediction Results
Figure 1. Market Cycle Prediction Results.

The prediction signals anticipate market conditions providing early warning investing and de-investing signals. A perfect market signal would be the mkt signal shifted one day earlier, i.e., mkt_1. Of course, this perfect signal does not exist but is useful for comparison. For the Bull-Bear-Bull market of 2020, the anticipatory market signals are summarized in the table below. A sell signal (mkt_1 = 0, or p_1 = 0 or p_1_s = 0) anticipates the market low. A buy signal (mkt_1 = 1 or p_1 = 1 or p_1_s = 1) attempts to provide an upmarket signal after and as close to the market close as possible. The perfect signal (mkt_1) anticipated the low by 24-days and provided a buy signal at end-of-day corresponding to the Bear market low. The p_1 signal anticipated downward trending market low by 22-days, and provided a buy signal 2-days after the Bear market low point. We also note that the p_1 signal had a short term buy-sell cycle because the market appeared to be turning up within the Bear period. We will see that p_1 is more profitable, but with potentially short-term cycles. The smoothed p_1_s signal anticipated the market low by 20-days and provided a buy signal 5-days after the market low.

Table 1: Prediction signals summary during the 2020 Bear market cycle.

Signal Date days from high days before/after low
mkt_1: 1 to -1 Feb 19, 2020 0-day 24-days before
p_1: 1 to 0 Feb 21, 2020 2-days 22-days before
p_1_s: 1 to 0 Feb 24, 2020 4-days 20-days before
mkt_1: -1 to 1 Mar 23, 2020 24-days 0-days after
p_1: 0 to 1 Mar 24, 2020 25-days 1-day after
p_1_s: 0 to 1 Mar 26, 2020 29-days 5-days after

Feature Importance

The ML dataframe load at the beginning of this exercise contained 52 columns, including the dependent variable, mkt. The number of features, and the specific features included, will vary for each model. 20 ML Features are selected for the best performing XG Boost model. The Feature selection results from an iterative process, including model training, removing low importance features, or features with high multi-collinearity until the model performance begins to suffer

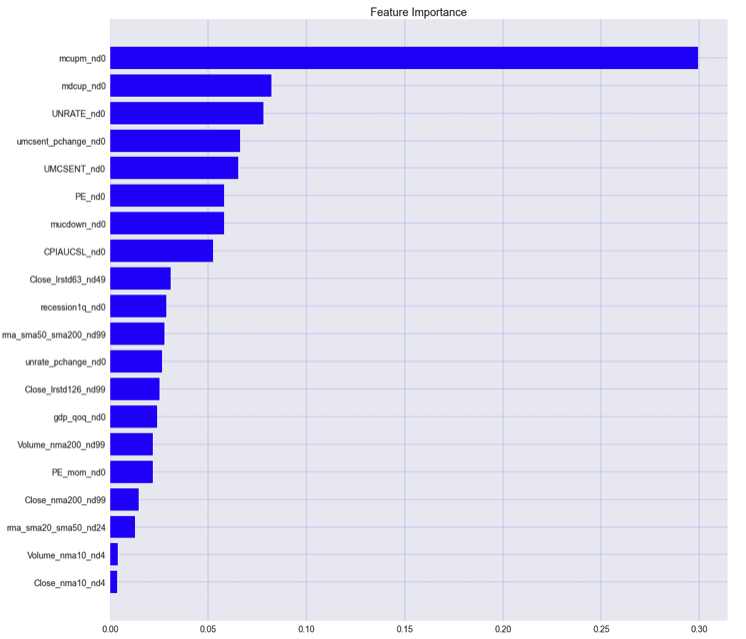
Market Cycle Prediction Results
Figure 2. Market cycle prediction XGB model feature importance.

The XGB model feature importance is illustrated in Figure 2. Each of the ML Features is described in the previous two articles. Below is a description and comments about these 20 ML variables. The “_nx” following each variable corresponds to the amount of shift it received for feature alignment.

Financial Backtesting

Financial Performance Tables

The Market Cycle model’s ultimate measure of value is the ability to generate superior returns, in this case relative to the S&P 500 index. The fmbacktest() receives an input dataframe with daily close prices and a trade signal. In this case we shift the p_1 or p_1_s and the variables become p and p_s. The fmbacktest() function receives as input the name of the “strategy” variable, which in our case is either p or p_s. If the strategy variable = 1, then the strategy investment receives a price change equal to the day’s market performance. The fmbacktest() function returns a summary dataframe with yearly results and a detailed dataframe with daily results. Each dataframe contains the S&P 500 returns and the strategy return achieved by applying the buy-sell signal p or p_s.

In the code block below, we provide as input the dfxyp dataframe (dataframe with x dependent variables, y dependent variable y, and prediction results) and indicate the name of the price variable, trade signal, p, and backtest start and end dates from 2020-1-1 to 2020-11-4. The results are listed below the code block. The S&P 500 index at the beginning of the period is \$3230.78. At the end of the period, the S&P 500 experiences the COVID Bear and then recovers, ending at \$3,443.78. Meanwhile, trading with the trade signal p achieves an ending value of \$4,912.49. Thus, trading with ML prediction signal results in a 52% increase over the period versus a 6.58% return for the S&P 500 index.

price_variable='Close'
se=(dt.datetime(2020,1,1),dt.datetime(2020,11,4))
dftsummary,dfbt=fmbacktest(dfxyp[se[0]:se[1]].copy(),price_variable,'p')
dftsummary.T
   
start_date 2020-01-01
end_date 2 020-11-04
start_price 3,230.78
end_price 3,443.44
start_strategyvalue 3,230.78
end_strategyvalue 4,912.49
r 0.0658
r_strategy 0.5205

Next, over the same period (2020-1-1 to 2020-11-4) the smoothed prediction signal, p_s is backtested. Recall that the p_s signal eliminates short-term buy-sell cycles. Often this is desired rather than making a short-term potentially large investment and de-investment. The p_s trade signal provides a return of 26.77% vs. 6.58% for the S&P 500 index. The smooth signal provides the benefit of eliminating short-term buy cycles at the cost of accuracy, which translates to reduced investment performance relative to the p raw model output.

price_variable='Close'
se=(dt.datetime(2020,1,1),dt.datetime(2020,11,4))
dftsummary,dfbt=fmbacktest(dfxyp[se[0]:se[1]].copy(),price_variable,'p_s')
dftsummary.T
   
start_date 2020-01-01
end_date 2020-11-04
start_price 3230.78
end_price 3443.44
start_strategyvalue 3230.78
end_strategyvalue 4095.63
r 0.0658231
r_strategy 0.2677

We next look at the performance over several years, from 2000 to 2020-11-4. Investing \$1469.25 in a market index at the beginning of the year 2000 results in \$3,443.44 by November 4, 2020. If the investment is managed with the p buy signal, the ending value is \$24,281. The year 2000 experienced a Bear market cycle, and S&P 500 lost 10% while the ML (p) returned 3.07%. The ML return is greater than the S&P 500 return for each year there is a Bear cycle - 2000, 2001, 2002, 2008, 2009, and 2020. For years without a Bear cycle, the S&P 500 market return, r, is identical to the strategy (ML) return, r_strategy.

    se=(dt.datetime(2000,1,1),dt.datetime(2020,12,31))
    dftsummary,dfbt=fmbacktest(dfxyp[se[0]:se[1]].copy(),price_variable,'p')
    dftsummary[['start_price','end_price','start_strategyvalue', 'end_strategyvalue', 'r', 'r_strategy']]

Table 2: Backtesting XGB Model prediction, p, 2000 - 2020-11-4

Year s_price e_price s_strategy_v e_strategy_v r r_strategy
2001 1469.25 1320.28 1469.25 1514.34 -0.1014 0.0307
2001 1320.28 1148.08 1514.34 1717.51 -0.1304 0.1341
2002 1148.08 879.82 1717.51 1817.85 -0.2337 0.0584
2003 879.82 1111.92 1817.85 2297.40 0.2638 0.2638
2004 1111.92 1211.92 2297.40 2504.02 0.0899 0.0899
2005 1211.92 1248.29 2504.02 2579.17 0.0300 0.0300
2006 1248.29 1418.30 2579.17 2930.43 0.1362 0.1362
2007 1418.30 1468.36 2930.43 3117.92 0.0353 0.064
2008 1468.36 903.25 3117.92 3531.58 -0.3849 0.1327
2009 903.25 1115.1 3531.59 5511.84 0.235 0.56073
2010 1115.1 1257.64 5511.84 6216.4 0.1279 0.1278
2011 1257.64 1257.6 6216.4 6216.2 -0.00003 -0.00003
2012 1257.6 1426.19 6216.2 7049.52 0.1341 0.1341
2013 1426.19 1848.36 7049.52 9136.27 0.2960 0.2960
2014 1848.36 2058.9 9136.27 10176.95 0.1139 0.1139
2015 2058.9 2043.9 10176.95 10103.00 -0.0073 -0.0073
2016 2043.94 2238.83 10103.00 11066.33 0.0954 0.0954
2017 2238.83 2673.61 11066.33 13215.41 0.1942 0.1942
2018 2673.61 2506.85 13215.41 12391.13 -0.0624 -0.0624
2019 2506.85 3230.78 12391.13 15969.44 0.2888 0.2888
*2020 3230.78 3443.44 15969.44 24281.98 0.0658 0.5205

Similarly, investing with the smoothed prediction signal p_s results in a gain relative to the S&P 500 index. The strategy return is always greater than the S&P 500 index return for years with a Bear cycle and equal to the S&P 500 index return for years without a Bear cycle. Investing \$1,469.25 in a market index on January 1, 2000 results in a value of \$16,885.39 on November 4, 2020, while the S&P 500 achieves a value of \$3,443.44.

    se=(dt.datetime(2000,1,1),dt.datetime(2020,12,31))
    dftsummary,dfbt=fmbacktest(dfxyp[se[0]:se[1]].copy(),price_variable,'p_s')
    dftsummary[['start_price','end_price','start_strategyvalue', 'end_strategyvalue', 'r', 'r_strategy']]


Table 3: Backtesting XGB Model smoothed prediction, p_s, 2000 - 2020-11-4
Year s_price e_price s_strategy_v e_strategy_v r r_strategy
2000 1469.25 1320.28 1469.25 1487.92 -0.1014 0.0127
2001 1320.28 1148.08 1487.92 1677.04 -0.130 0.1271
2002 1148.08 879.82 1677.04 1740.73 -0.233 0.0379
…            
*2020 3230.78 3443.44 13319.79 16885.39 0.0658 0.2677

*2020 data up to 2020-11-4

Financial Performance Graphs

The next set of graphs provide visualizations of the financial performance over different periods.

The first set of graphs, figure 3 (a) - 3 (d), demonstrate the performance from the year 2000 (January 1) to November 4, 2020. The results of several models are compared, including an XGB (XG Boost Model), RF (Random Forest), and DT (Decision Tree), relative to the S&P 500 market performance. We make the following observations.

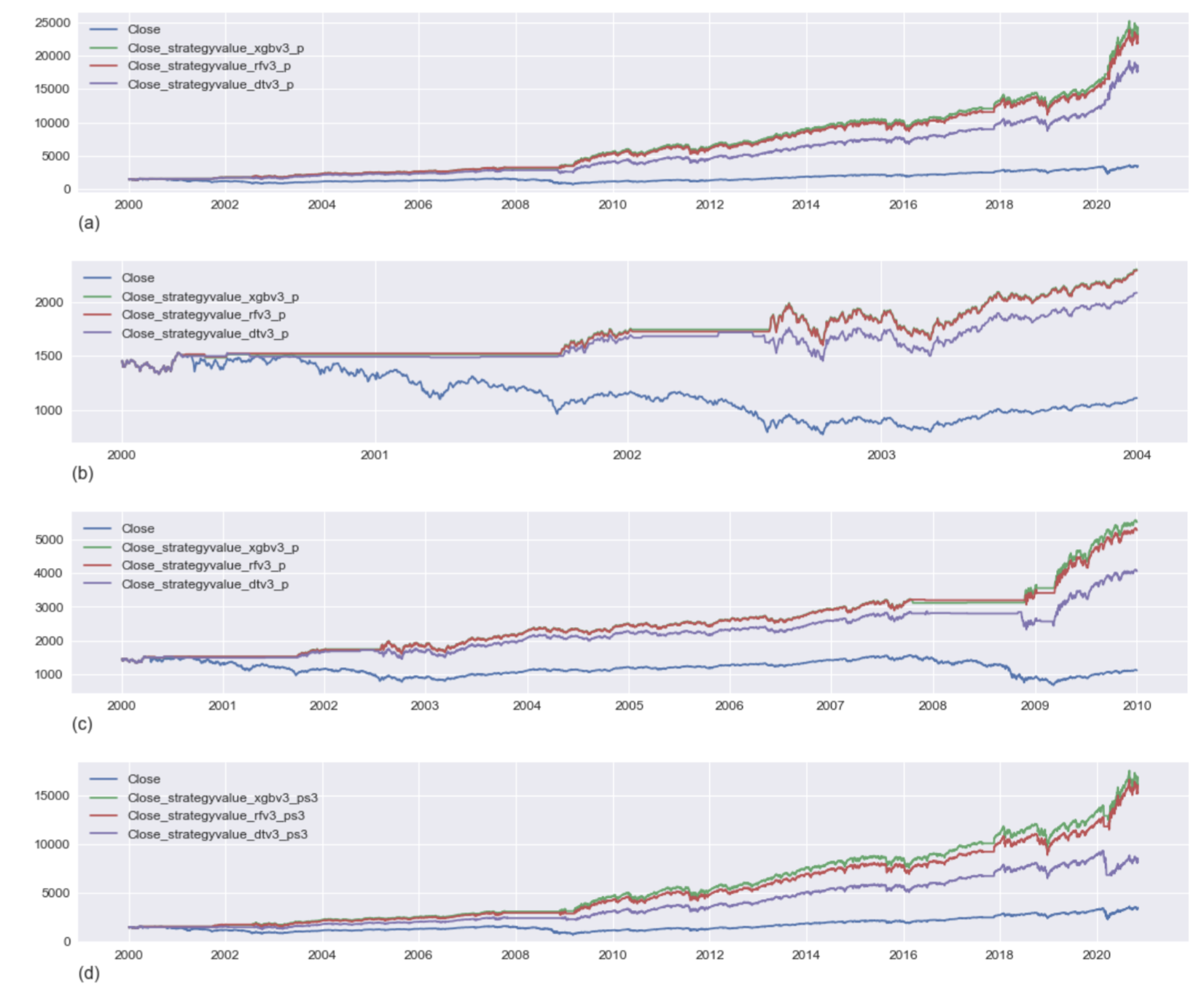
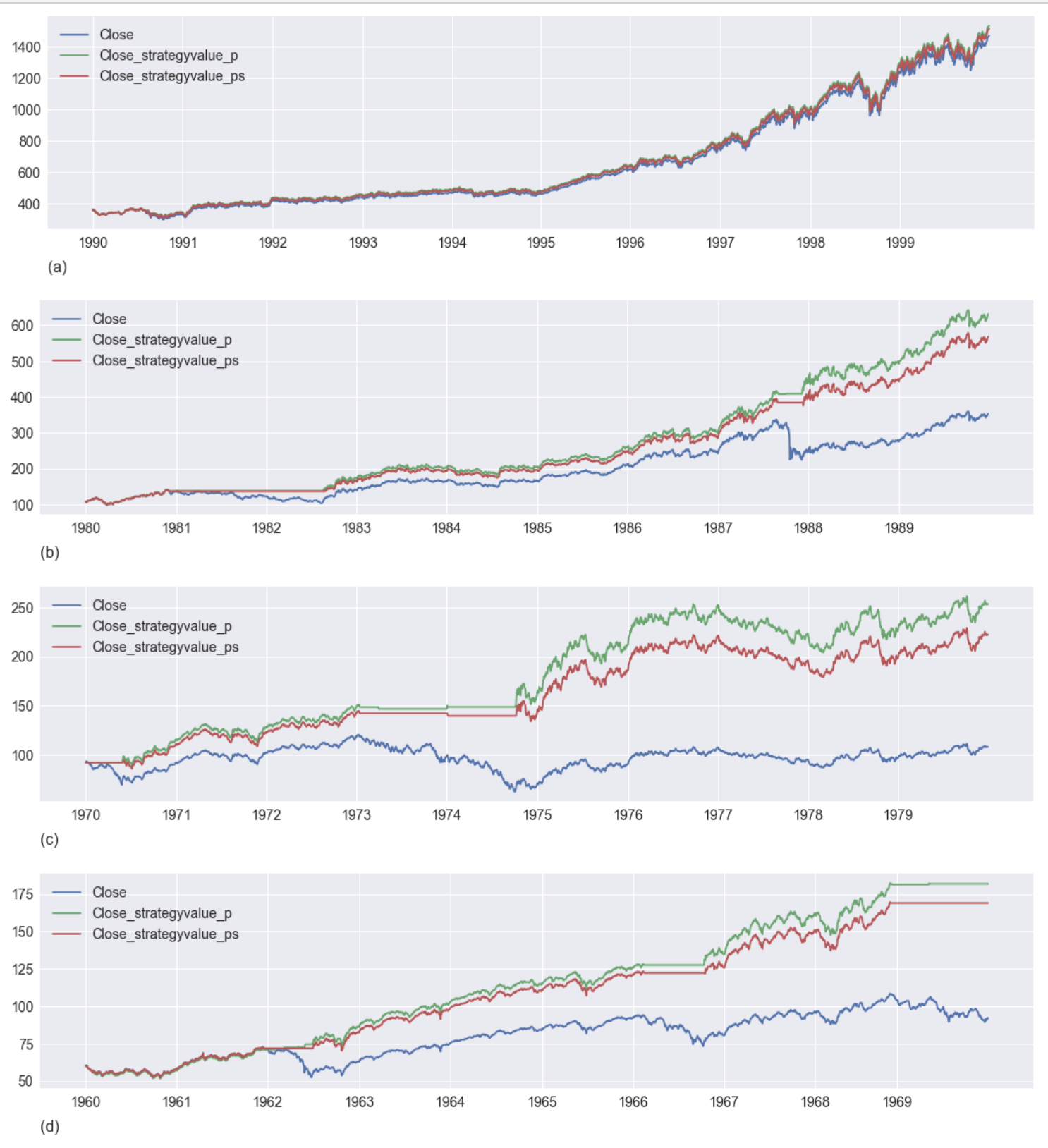
Market Cycle Prediction Results
Figure 3. Market cycle prediction (XGB, RF, DT) backtest 2000 to 2020-11.

Figure 4 (a - d) illustrate the performance of the XGB model (p and p_s) predictions for each decade 1990 (a), 1980 (b), 1970 (c), and 1960 (d). The following observations are made.

Market Cycle Prediction Results
Figure 4. Market cycle prediction (XGB) backtest for decades 1990 (a), 1980 (b), 1970 (c), 1960 (d).

Summary and Conclusions

The key objectives of this exercise are to develop an ML model for predicting Bear and Bull market cycles, build the model based on open-source data, and contribute the corresponding software to open-source. Addressing these objectives is described in three articles, summarized below.

First Article - Analyzing Bear and Bull Markets in Python. In this article, the fmcycles() function for analyzing Bear and Bull market cycles is introduced. The Bear (downward trending) and Bull (upward trending) cycles are identified from daily stock data. A classic Bull and Bear market annotated chart with normalized market cycle returns are graphed with the fmplot() function. Several variables useful as ML are derived by the fmplot() function, including mkt the market cycle truth variable (dependent variable, label), mcupm a delayed version of mkt useful, mdcup the price percent increase from the previous market low during a Bear cycle, and mucdown the price percent decrease from the previous market high during a Bull cycle.

Second article - Market Cycle Prediction Model - Data Analysis. After establishing the objectives (business and technical), data wrangling and exploratory data analysis are the first steps to developing an effective ML model. Data is input from a few open-source APIs with the help of the fmget module, including Yahoo Finance, Quandl, and FRED. Financial data includes:

With the functions included in the fmtransforms module, the data is analyzed, merged, and transformed into a single dataframe representing a set of ML Features, one row per market day. Data analysis includes analysis of feature correlations and time alignment, which are essential for feature selection and feature alignment during model building. The ML dataframe is saved for subsequent use in developing the ML model.

Third article (this article) - Market Cycle Prediction Model. This article is the last in the series and describes developing and testing the ML model. The model development process begins with loading the ML dataframe saved in the previous step. Several functions from the fmml module are employed to develop the ML model. Features are aligned with the malign() function, The fmclftraintest() function manages model training and test process, and model performance is reported with the fmclfperformance() function. Several tree-based ML models are trained and tested. These include Decision Tree, Random Forest, and XG Boost. Feature selection resulted in 20 ML Features (predictor variables) for the XG Boost model (the best performing model). The model successfully achieves an impressive set of performance measures, including a high accuracy (99.5%), recall (98.2%), precision (98.7%), f1-score (98.4%), and successfully anticipates Bear and Bull market cycles from 1957 through 2020. The models are backtested with the use of the fmbacktest() function and are shown to provide a significantly better return compared to the S&P 500 index.

The three objectives set out at the beginning of the process are satisfied. The software introduced is available on Github - Pyquant. All data used in the modeling process is acquired from open-source APIs. A market cycle prediction model is developed and shows significantly improved financial returns relative to the S&P 500 market index.

There are several potential improvements to the market cycle prediction model, including modern NLP sentiment predictions and potentially better data sources. Additionally, the methods developed so far can be extended to modeling securities, and to include other investment strategies.